How to achieve Pareto-optimal Allocation between two consumers?

First of all, what is a Pareto-optimal situation?

It is a situation in which no consumer can be made better off without making anyone else worse off. In economics, a situation that is not Pareto optimal implies that a certain reallocation of goods may result in some individual being made better off without making the other worse off. Hence, situations that are not Pareto optimal are to be avoided. (From Wikipedia, Pareto Efficiency)

But how to achieve Pareto-optimality?

To explain this, I make use of lecture slides from my Intermediate Microeconomics course at LUMS with Dr. Ali Hasanain. Lets assume that there are two consumers: A and B and their endowments of goods 1 and 2 are:

To show this in a diagram, I will use the Edgeworth box, which was devised by Edgeworth and Bowley to show all possible allocations of goods 1 and 2 between the two consumers. Lets see how to start with it:

Now, what allocations of 8 units of good 1 and 6 units of good 2 are feasible? How can all feasible allocations be depicted by the edgeworth box?
Basically, all points in the edgeworth box, including the boundary, represent feasible allocations between the two consumers. But which allocation can lead to a Pareto improvement i.e. which allocation can make both consumers better off?

To answer the question, we need to add preferences to the box. In economics, preferences are modelled by indifference curves which are set of all bundles of goods between which a consumer is indifferent i.e. these bundles are equally preferred by the consumer. For further elaboration on this concept, visit Indifference curve

Now, drawing the indifference curves for both A and B, we obtain:

All bundles above the indifference curves are more preferred. Now flipping the axes for B, and arranging both indifference curves together in the edgeworth box we obtain:

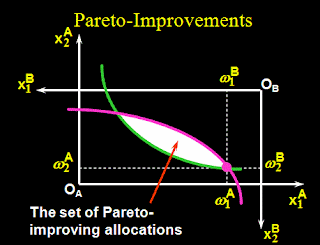
Now lets figure out the Pareto improving allocations. All points in the box, that lie above the indifference curves for both consumers represent Pareto improving situations, since they are preferred by both consumers simultaneously, as shown in the diagram below:

But which Pareto improving allocation will be the outcome of trade?

Now lets take a closer look at the indifference curves and find the situation that is Pareto optimal:

The above diagram shows the directions in which one consumer is better off and the other is worse off, as well as where both are worse off. Now coming back to our questions: which situation is Pareto optimal?

Here is the answer:

Therefore, an allocation where convex indifference curves are "only just back to back" is Pareto-optimal!                    

Reference:

• Pareto Efficiency, Wikipedia                                                                 http://en.wikipedia.org/wiki/Pareto_optimality
• Indifference Curve                                                                               http://en.wikipedia.org/wiki/Indifference_curve
• Lecture Slides by Dr. Ali Hasanain. Intermediate Microeconomics. Spring Semester 2010-2011.